Stat110 - Introduction to Probability代码的R语言与Python实现

这篇文章主要是用于记录将哈佛大学Stat110的教材用书《Introduction to Probability》第一版一书中的R代码向Python进行翻译转换，相关资源链接：http://stat110.net

  本博文还在更新中，最新更新为27/04/2020, Chapter05，出于一些原因，暂时停更。建议你使用能够支持markdown的浏览器，如新版本chrome或edge来进行阅读，否则可能出现格式错乱问题。在完成以后会提供全文pdf文件。

  R语言在科学计算上的确有很多优势，但是学习起来学习曲线比较陡峭，不太适合新手。我用惯了Python，想要同时把他们两都操作一下熟悉熟悉。以后的代码对比都以下面的形式或者表格形式来展现。国内需要使用R的话，建议直接到清华镜像下载：https://mirrors.tuna.tsinghua.edu.cn/CRAN/

  注意：本博文只对书本上的代码进行介绍与翻译，对其相应的知识点只会粗略带过，需要读者自行进行学习。

Chapter 01

  对应原文1.8内容。

  第一章总结：

  第一章主要讲了一些基础的概率论知识，诸如：朴素概率定义（其实就是古典概型）和他的一些重复运算的解决方法，以及一些概率的性质而已。

  比较特别的是，第一单元里讲了一些Story Proof（故事论证）之类的东西让一些二项式系数公式的记忆变得尤为方便，而且里面举的很多例子都是很好帮助理解的内容，这是跟国内的教学差别很大的地方。

向量

Python：

v = np.array([3,1,4,1,5,9]) # 将v定义为一组向量[3,1,4,1,5,9]

R：

v <- c(3,1,4,1,5,9) # 将v定义为一组向量(3,1,4,1,5,9),c代表concatenate

  在Python里面此处用Numpy的数组做向量。与Python不同，R语言是建立在向量之上的，就算是简单的 n <- 100 都被R视为一个长度为1的向量。

  当然在R里面稍有不同的是，”=”与”<-“使用上稍有不同，在函数调用中，func(x=1)与func(x<-1)是有区别的，前者调用完后变量x不会被保留，而后者会在工作区里保留变量x=1。

  R与Python不同的地方还是有挺多的：

Python	R	效果
sum(v)	sum(v)	求和
max(v)	max(v)	求最大值
min(v)	min(v)	求最小值
len(v)	length(v)	获得长度
range(m,n+1)	m:n	m,m+1,…n-1,n

  在元素获取上，两者区别还是挺大的，最大区别还是从0还是1开始数：

Python	R	输出
v[0]	v[1]	3
？（Python有吗）	v[-(2:4)]	1 5 9
v[[0,2,4]]	v[c(1,3,5)]	[3,4,5] / 3 4 5
[x**(-2) for x in range(1,101)]	1/(1:100)^2	$(\frac{1}{1^2},\frac{1}{2^2},…,\frac{1}{100^2})$

阶乘与二项式

  在本来并不用于计算的Python中，运算这种需要调用别的库，例如阶乘：

Python：

import math
math.factorial(n)

R：

factorial(n)

  同样的也有像二项式，一般Python图方便会直接自己写一个函数，不过实在要调用也是可以的。

Python

from scipy.special import comb
comb(n,k)

R：

choose(n,k)

  R相较之下真的太方便了。此外R还有lchoose(n,k)，lfactorial(n)用来运算log值，方便进行乘法转换加法。

取样模拟

  这方面二者用法是很相似的，直接上表格吧。

Python	R	效果
np.random.choice(range(1,n+1),size=k,replace=False)	sample(n,k)	从1-n中不放回抽样k次
np.random.choice(range(1,n+1),size=k)	sample(n,k,replace=True)	从1-n中有放回抽样k次
np.random.choice([‘a’,’b’,…,’z’]),size=k,,replace=False)	sample(letters,k) #letters是R自带的26个小写字母表数组	从26个字符中取不重复地取字母组成k字符单词
np.random.choice(range(1,5),size=3,replace=False,p=[0.1,0.2,0.3,0.4])	sample(4, 3, replace=TRUE, prob=c(0.1,0.2,0.3,0.4))	1-4的概率分别为0.1,0.2,0.3,0.4

de Montmort‘s 配对问题

  de Montmort’s配对问题指的是一堆卡片标有1-n的数字，打乱后一张一张的掀开，第k次掀开的若对应的数字正好为k，那么则视为成功，求的是整套卡片翻完的至少成功一次的概率。

  单纯的运算需要运用Inclusion-exclusion公式：

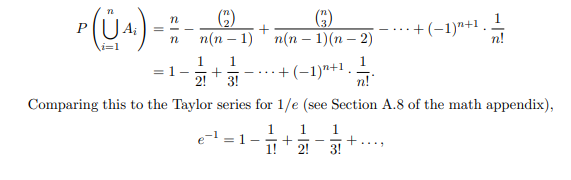
  而在代码里我们可以做simulation模拟。

Python：

n = 100
count = 0
for i in range(10**4):
    r = sum(np.random.choice(range(1,n+1),n,replace=False)==range(1,n+1))
    if r>=1:
        count+=1

print(count/10**4)

R：

n <- 100
r <- replicate(10^4,sum(sample(n)==(1:n))) # 重复10^4次，计算n个不重复取样与1:n的相同个数总数
sum(r>=1)/10^4

  R是真的简短很多，不愧是数字科学专用语言…不过说真的，python的代码相比之下更加友好。

生日问题

  对于生日问题的概率计算，Python，所幸numpy也支持prod。

Python：

1-np.prod((365-k+1,365+1))/365**k

R的话有两种方式：

1-prod((365-k+1):365)/365^k # 1.直接计算
pbirthday(k) # 2.使用内置的函数

  还挺犯规的，生日问题都内置了。而且R还能用qbirthday(n)来计算达到n概率两人以上相同生日所需要的人数。而且对于这两个函数，还能加上coincident参数来指定特定多少人同一天生日，在这就不做示范了。

  生日问题的模拟的话是这样：

Python：

count = 0
for i in range(10**4):
    if Counter(np.random.choice(range(365),23)).most_common(1)[0][1]>1:
        count += 1
print(count/10**4)

R：

r <- replicate(10^4, max(tabulate(sample(1:365,23,replace=TRUE)))) # 重复10^4次，计算23次从365个数重复取样取得相同次数最多的个数
sum(r>=2)/10^4

Chapter 02

  对应原文2.10的内容

  第二章总结：

  这一章很细致的讲了条件概率的各种东西，包括事件独立性，贝叶斯，全概率公式，多条件概率，条件的选择（三门问题，递归问题，Gambler’s ruin）各种谬误（Prosecutor’s fallcay，Simpson’s paradox)。

  内容都十分深入浅出，有一说一，相比起国内大学蓝色那本概率统计真的细致太多了。

模拟频率派的理解

  这里用到书上的例子：

  一个家庭两小孩（$A$和$B$），在 ($C_1$) 已知至少有一个是女孩 和 ($C_2$) 已知有一个姐姐 分别的条件下，求两人都是女孩的条件概率，设事件$S$为两人都是女孩。

  这道题实际上就是求$P(S|C_1)$和$P(S|C_2)$。且因为前者是$\frac{1}{3}$而后者为$\frac{1}{2}$，让人觉得这道题的答案比较反直觉，但是其实却很合理。频率派的理解就是用大量实验去叠，那只需要取很多（这里取了$10^5$）个样就行。

Python:

n = 10**5
childa = np.random.choice([1,2],n,True)
childb = np.random.choice([1,2],n,True)
a = (childa==1) # 小孩A是女孩
b = (childb==1) # 小孩B是女孩
n_c1 = sum(a|b) # 至少一个女孩
n_s = sum(a&b) # A和B都是女孩
n_c2 = sum(a) # A是女孩
p_1 = n_s/n_c1 # P(S|C1)
p_2 = n_s/n_c2 # P(S|C2)
print('P(S|C1)=%f,P(S|C2)=%f' % (p_1,p_2))

R：

n <- 10^5
childa <- sample(2,n,replace=TRUE)
childb <- sample(2,n,replace=TRUE)
n.b <- sum(childa==1) # A是女孩
n.b2 <- sum(childa==1 | childb==1) # 至少一个女孩
n.ab <- sum(childa==1 & childb==1) # A和B都是女孩
n.ab/n.b # P(S|C2)
n.ab/n.b2 # P(S|C1)

  得到两个值一个接近0.33，另一个接近0.5，模拟完成。

三门问题模拟

  三门问题又称Monty Hall问题，比较经典的一个条件概率问题，在这里就不介绍了上网可以查到，可能之后会补充。先放一个书上的R语言版本，他加了一点交互式来进行模拟游戏：

monty <- function() {
    doors <- 1:3

    # randomly pick where the car is
    cardoor <- sample(doors,1)

    # prompt player
    print("Monty Hall says ‘Pick a door, any door!’")

    # receive the player’s choice of door (should be 1,2, or 3)
    chosen <- scan(what = integer(), nlines = 1, quiet = TRUE)

    # pick Monty’s door (can’t be the player’s door or the car door)
    if (chosen != cardoor) montydoor <- doors[-c(chosen, cardoor)]
    else montydoor <- sample(doors[-chosen],1)

    # find out whether the player wants to switch doors
    print(paste("Monty opens door ", montydoor, "!", sep=""))
    print("Would you like to switch (y/n)?")
    reply <- scan(what = character(), nlines = 1, quiet = TRUE)

    # interpret what player wrote as "yes" if it starts with "y"
    if (substr(reply,1,1) == "y") chosen <- doors[-c(chosen,montydoor)]

    # announce the result of the game!
    if (chosen == cardoor) print("You won!")
    else print("You lost!")
}

  R的代码用来写这种程序实在是…有点尴尬，交互和代码可读性过于差了。我的话，是尝试利用频率派的方式模拟，来计算多次三门问题分别在使用了 策略1： 一直换门 和 策略2：绝不换门 之下的概率，感觉这样对比更有实际意义。

Python：

import random

def MontyHall(n_select, is_change):
    n_car = random.randint(1, 3)
    if n_select == n_car:
        if is_change:
            return False
        else:
            return True
    else:
        if is_change:
            return True
        else:
            return False

# strategy of always changing doors    
count = 0
for i in range(10**5):
    n_select = random.randint(1, 3)
    if MontyHall(n_select, True):
        count += 1
print('Prob of changed', count/10**5)

# Strategy of always NOT changing doors   
count = 0
for i in range(10**5):
    n_select = random.randint(1, 3)
    if MontyHall(n_select, False):
        count += 1
print('Prob of not changed', count/10**5)

R：

monty <- function(n_selected, is_change) {
    n_car <- sample(3,1)
    if(is_change){
        if(n_car == n_selected){
            return(FALSE)
        }else{
            return(TRUE)
        }
    }
    else{
        if(n_car == n_selected){
            return(TRUE)
        }else{
            return(FALSE)
        }
    }
}

# Strategy of always changing doors
r <- replicate(n=10^4,monty(sample(3,1),TRUE))
sum(r/10^4)

# Strategy of always NOT changing doors
r <- replicate(n=10^4,monty(sample(3,1),FALSE))
sum(r/10^4)

  得到两个值一个接近0.33，另一个接近0.66，完事了。

  不过从这代码啊就可以看出来，Python相较于R还是更加万金油一点，Python写循环写嵌套都是比较清晰的，R这个语法就写这么个小函数却实在把用惯Java，Python之类语言的我糊弄的难顶。（扶额）

Chapter 03

  对应原文3.11内容。

  第三章总结：

  第三章开始讲随机变量了，这一章和下一章好像都是只讲离散型。

  这一章只讲了几个常见离散分布，除了Bernoulli和Binomial以外，还有一个在国内大学概率论好像不接触，叫超几何分布HyperGeometric，虽然听的挺多但是正式去了解还是第一次。

  印象中除了这些分布以外，还有他讲的内容也很特别。例子有很多，包括PMF，CDF的定义证明之类的，上面三个分布的联系之类的，不过让我印象最深刻的还是他给随机变量与分布关系的定义：

分布之于随机变量，就像蓝图之于房子。不同的房子可以用同样的蓝图，而不同的随机变量也能有相同的分布。

  书本内容真的很深入浅出，不过继续代码吧。（本章代码省略了离散型均匀分布部分，那部分连Stat110上课都没讲，因为无非就是古典概型取样，可以参照第一章内容）

二项分布

  贝努利分布就没必要整了，就是一次二项分布。以在$X\sim{Bin(5,0.2)}$当$X=3$为例子。

  （国内一般用的标识应该是$X\sim{B(5,0.2)}$）

Python：

# Python需要用到scipy的stats模块
from scipy.stats import binom
print('P(X=3):',binom.pmf(3,5,0.2),'\nF(X=3):', binom.cdf(3,5,0.2))
print('Samples of X~Bin(5,0.2)',binom.rvs(size=7,n=5,p=0.2))

# 输出：
> P(X=3): 0.051200000000000016 
> F(X=3): 0.99328
> array([2, 1, 1, 1, 1, 2, 0])

R:

dbinom(3,5,0.2) # PMF
pbinom(3,5,0.2) # CDF
rbinom(7,5,0.2) # 从分布中随机取样7个

#输出
[1] 0.0512
[2] 0.99328
[3] 1 2 1 2 3 2 2

  很显然，R的代码辨识度是真的不好。相比之下Python用户体验还是很好的，难怪支持者两极分化严重。

超几何分布

  废话不多说，对于PMF，CDF和取样的做法大同小异，要不是书上有我也不写了，直接上表格算了。

  超几何分布标识一般是这样$X\sim{HGeom(w,b,n)}$，不过也有是这样标识的$X\sim{G(n,M,N)}$，这两种标识正好代表了在R和在Python里的不同用法。（R是用第一个，而Python是第二个）

  先简单的说明一下，超几何分布其实就是不放回取样的成功数。而$X\sim{HGeom(w,b,n)}$里，$w$代表了所有样本中成功的样本数，$b$代表所有样本中失败的样本数，$n$代表取样的数目。而在标识$X\sim{G(n,M,N)}$里，$n$还是代表取样本数，而$M$代表所有样本数，$N$表示成功的样本数。

  的确有所区别，不过大同小异，Python的话记得import调包就完事了。

Python	R
hypergeom.pmf(k=5,n=8,M=30,N=10)	dhyper(5,10,20,8)
hypergeom.cdf(k=5,n=8,M=30,N=10)	phyper(5,10,20,8)
hypergeom.rvs(size=10,n=8,M=30,N=10)	rhyper(10,10,20,8)

Chapter 04

  对应原文4.11内容。

  第四章总结：

  第四章整的东西还挺多，把全部常用的离散型分布给讲完了，而且还挺多的，包括几何分布、第一次成功分布、负二项分布和泊松分布，还有诸如期望、方差的定义与性质。这一章最有意思的还是一个随机变量标识器（Indicator r.v.s）的思想，在分析的时候尤其是对期望分析的时候特别有用。

几何分布、负二项分布、泊松分布

  因为第一次成功分布（First Success Distribution)就是几何分布的随机变量加一，没什么好说的，就先把这三个简单罗列一下吧。Python同样使用的是Scipy.stats模块。

Python	R	Distribution
geom.pmf/cdf/rvs	d/p/rgeom	$X\sim{Geom(p)}$
nbinom.pmf/cdf/rvs	d/p/rnbinom	$X\sim{NBin(r,p)}$
possion.pmf/cdf/rvs	d/p/rpois	$X\sim{Pois(\lambda{})}$

求期望

  书上是直接用了第一章Matching Problem的例子来求期望。按道理这里的期望模拟得到会十分接近于 1，至于为什么有兴趣的各位请看书吧，在Example 4.4.4上利用了随机变量标识器来进行计算得到的。

Python:

n = 100
count = 0
r = []
for i in range(10**4):
    r.append(sum(np.random.choice(range(1,n+1),n,replace=False)==range(1,n+1)))
print(np.mean(r))

R:

n <- 100
r <- replicate(10^4,sum(sample(n)==(1:n)))
mean(r)

另一个生日问题模拟

  这一个生日问题来自Example 4.4.5，也是一个随机变量标识器的例子。意思是有n个人，求365天里至少有一人生日的日子数的期望值。这个值会无限接近于$365(1-(\frac{364}{365})^n)$，这里例子取$n=20$。

Python:

import numpy as np
k = 20
r = []
for i in range(10**4):
    r.append(len(np.unique(np.random.choice(range(1,365+1),k,True))))
print(np.mean(r))

R:

k <- 20
r <- replilcate(10^4, {bdays <- sample(365,k,replace=TRUE); length(unique(bdays))})
mean(r)

Chapter 05

  对应原文5.9内容。

  第五章总结：

  第五章完成了基本上是这个课程的一半了，内容还不少。虽然这篇博文注重代码，但还是把一个很重要的表格(见下图)放上来一下。这一章讲的是连续型随机变量以及各种连续型分布，包括均匀分布、Logistic分布、Rayleigh分布、正态分布与指数分布，还稍微提了提泊松过程。

  这一章比较重点的内容是：位置-刻度转换思想(Location-scale transformation)，均匀分布的普适性(Universality of the Uniform)

均匀分布、正态分布、指数分布等

  把这几个简单罗列一下吧。Python同样使用的是Scipy.stats模块。在命名上和上一次的超几何分布的参数上就可以看出来R语言很倾向数学上的命名法，不过暂时我没找到R写的Rayleigh分布。

Python	R	Distribution
uniform.pmf/cdf/rvs	d/p/runif	$X\sim{Unif(a,b)}$
norm.pmf/cdf/rvs	d/p/rnorm	$X\sim{N(\mu,\sigma^2)}$
expon.pmf/cdf/rvs	d/p/rexp	$X\sim{Expo(\lambda)}$
logistic.pmf/cdf/rvs	d/p/rlogis	$X\sim{Logistic}$
rayleigh.pmf/cdf/rvs	?	$X\sim{Rayleigh}$

  顺便在这里用正态分布表演一个location-scale变换。

  由$\frac{X-\mu}{\sigma}\sim{N(0,1)}$来获得$X\sim{N(\mu,\sigma^2)}$，此处$\mu=1$，$\sigma=2$。

Python:

import matplotlib.pyplot as plt
mu = 1
sigma = 2
x = mu + sigma * norm.rvs(size=10**4)
plt.hist(x) # 效果如下图

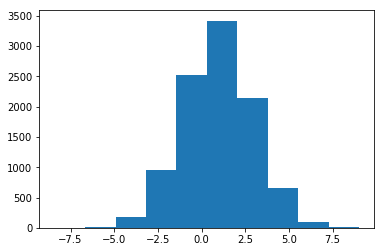
R:

mu <- 1
sigma <- 2
x <- mu + sigma * rnorm(10^4)
hist(x) # 效果如下图

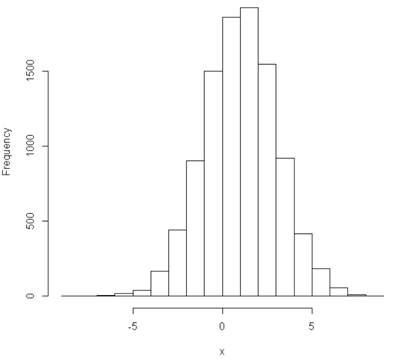
  R和Python在这方面上几乎完全一致，不用怎么翻译就很舒服。

画曲线

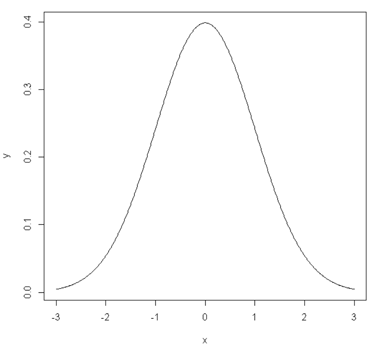
  再用标准正态分布在[-3,3]上的图整个pdf。

Python:

x = np.arange(-3,3,0.01)
y = norm.pdf(x)
plt.plot(x,y) # 效果如下图

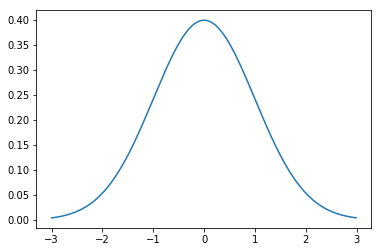
R有两种方式:

# 第一种跟Python一样
x <- seq(-3,3,0.01)
y <- dnorm(x)
plot(x,y,type='l')

# 第二种：R独有的
curve(dnorm, from=-3,to=3,n=1000) # 效果如下图

均匀分布的普适性模拟

  这里用Logistic分布来实现普适性的一个效果，即$log(\frac{U}{1-U})\sim{Logistic}$。

Python:

import numpy as np
from scipy.stats import uniform
from scipy.stats import logistic
import matplotlib.pyplot as plt

plt.figure(figsize=(13, 5)) #调整图像大小

# 使用普适性
u = uniform.rvs(size=10**4)
x = np.log(u/(1-u))
plt.subplot(1,2,1)
plt.hist(x,bins=20)

# 直接获取分布
plt.subplot(1,2,2)
x = np.arange(-10,10,0.01)
y = logistic.pdf(x)
plt.plot(x,y)
plt.show()

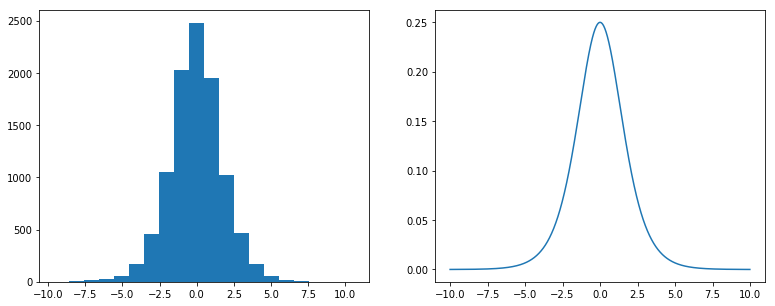
R:

# 使用普适性
u <- runif(10^4)
x <- log(u/(1-u))
hist(x)

# 直接获取分布
curve(dlogis, from=-15,to=15,n=1000)

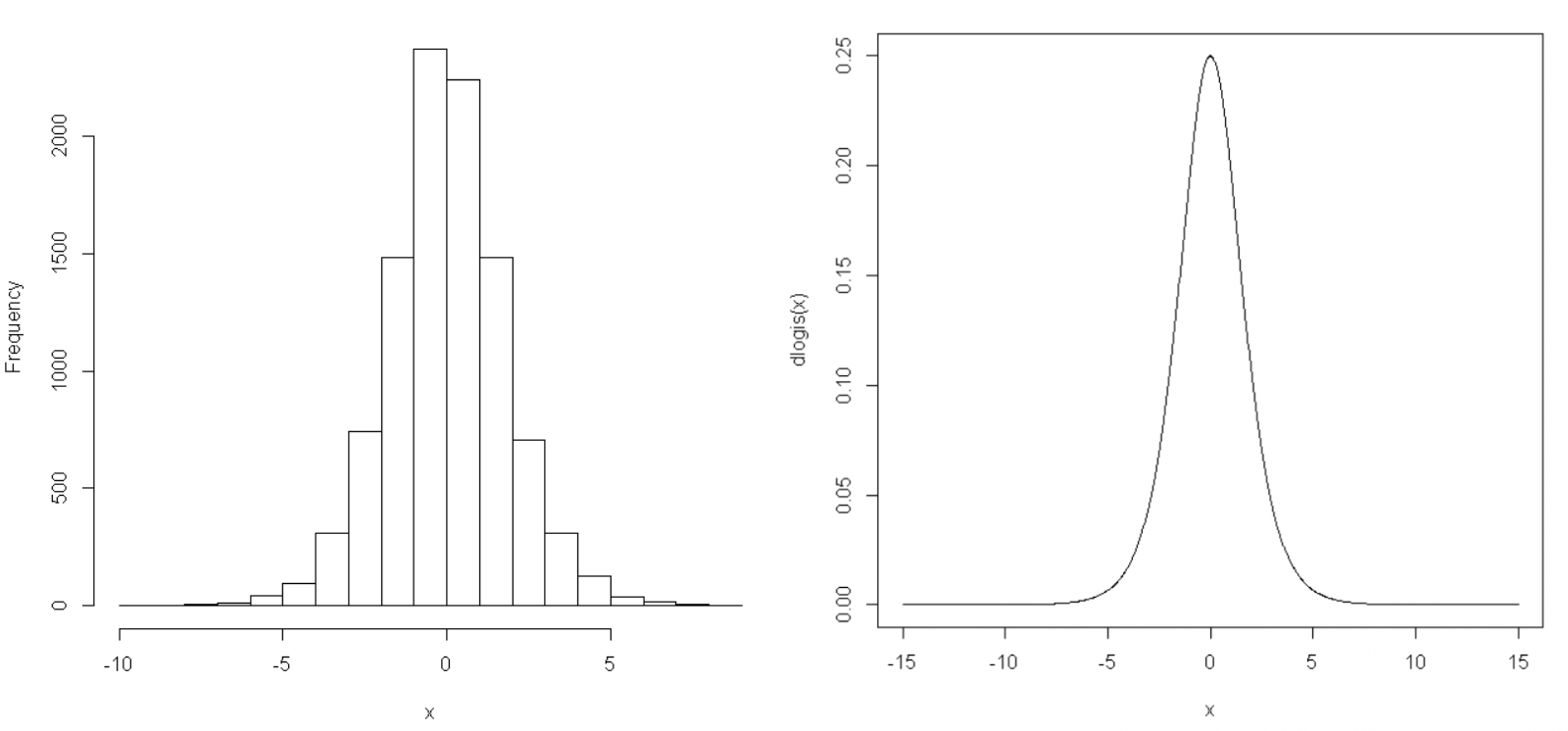
  反正就是输出跟直接获取分布走势很像，就模拟认为他可行了。

泊松过程模拟与验证

  指数分布与泊松分布有联系。指数分布每一个值是发生下一次无记忆性事件的时间点，所以是连续的。泊松分布可以视作单位时间内发生事件的次数。那么，对于rate为$\lambda$的泊松过程，会有，

• 间隔为1的时间段内发生事件的次数服从$Pois(\lambda)$

• 每次事件发生的时间间隔服从$Expo(\lambda)$

  下面来用指数分布生成时间间隔的方式验证”时间段内次数服从泊松分布”：

Python:

import numpy as np
from scipy.stats import expon
from scipy.stats import poisson
import matplotlib.pyplot as plt

plt.figure(figsize=(13, 5)) #调整图像大小

# 泊松过程
lamb = 10
r = []
for i in range(10**4):
    r.append(sum(np.cumsum(expon.rvs(size=20,scale=1/lamb))<1))
plt.subplot(1,2,1)
plt.hist(r,bins=20)

# 泊松分布
x = list(range(21))
y = poisson.pmf(x,mu=lamb)
plt.subplot(1,2,2)
plt.plot(x,y)
plt.show()

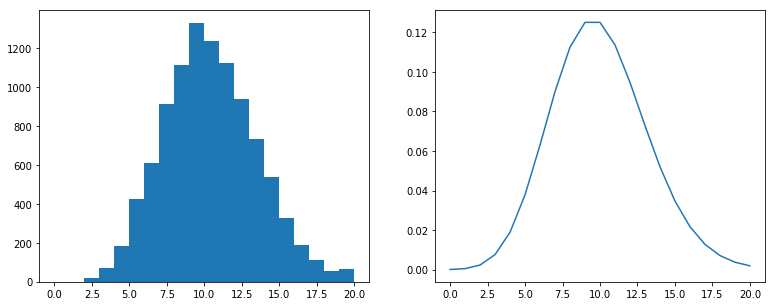
R:

# 泊松过程
lambda = 10
r = replicate(10^4,sum(cumsum(rexp(20,lambda))<1))
hist(r)

# 泊松分布
x <- 0:20
y <- dnorm(x,lambda)
plot(x,y,type='l')

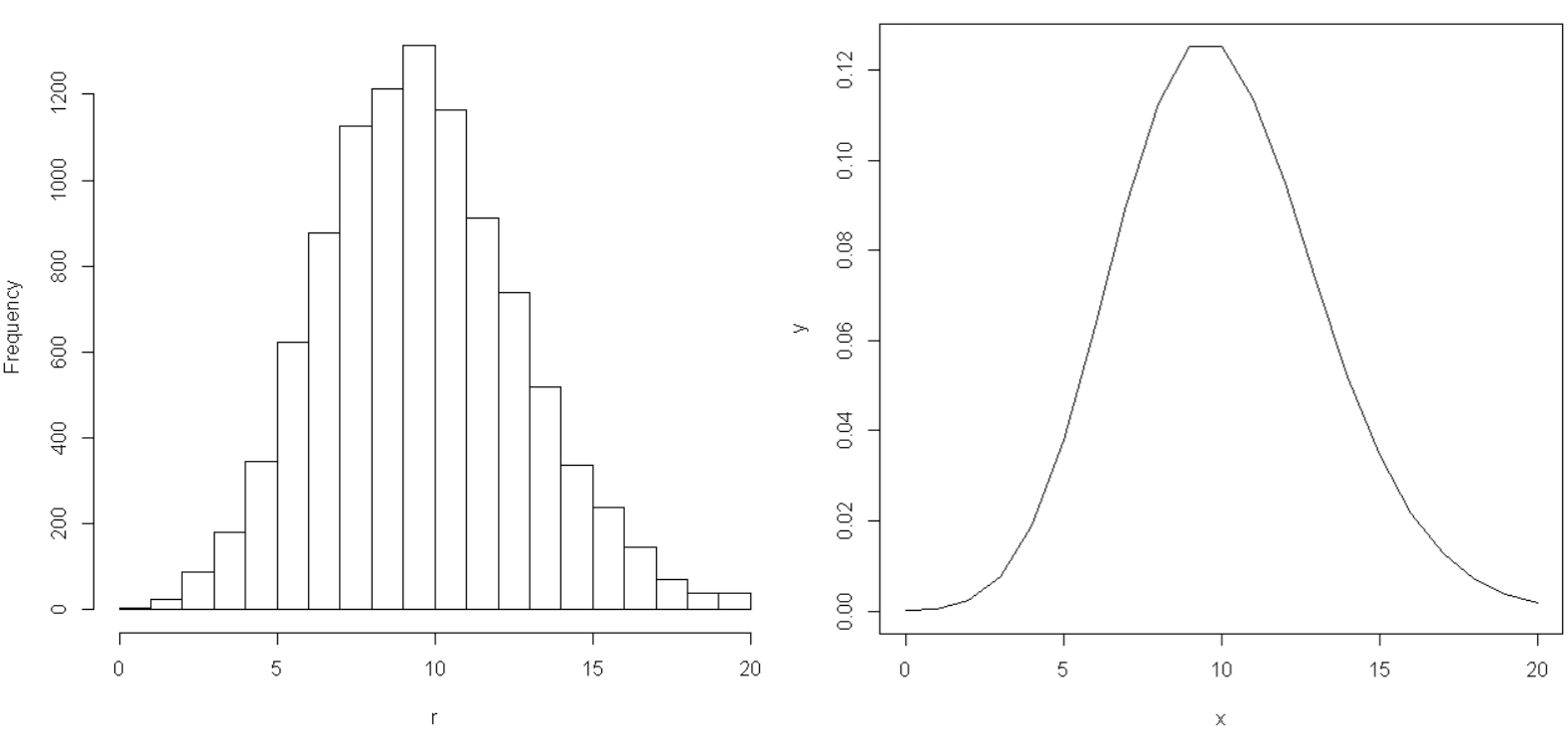
  图像都接近，完事了。

  要注意的是，对于Python与R的pmf函数，pdf函数之类的，参数都不太一样，所以必须要看清楚再输入。举这里的例子：

  在Python中，指数分布的pdf/cdf/rvs调整参数是通过location-scale转换来调整的，这是他的参数：expon.pdf(x,loc=0,scale=1)。

  所以我为了获得$\lambda=10$的指数分布，输入了scale=1/10。

  而在R中，参数是这样的dexp(k,rate=1)，那么直接输入rate=10即可。

  同理，对于泊松分布，Python里要输入参数的也不是$\lambda$，而是$\mu=\lambda t$。所以在这里我们取单位时间1，这时$\mu=\lambda$。而R中直接就是输入$\lambda$的值作为参数即可。二者区别还是很大的，总而言之还是R偏向数学用语。

  对于泊松过程详细内容请尽量参考书本或别的资料，在此不会详细解释。